 |
Abstract. Given r ≥ 3, we prove that there exists λ > 0 depending only on r so that if G is a metric graph of rank r with metric entropy 1, then there exists a proper subgraph H of G with metric entropy at least λ. This answers a question of the second two authors together with Rieck. We interpret this as a graph theoretic version of the Bers Lemma from hyperbolic geometry, and explain some connections to the pressure metric on the Culler−Vogtmann Outer Space. |
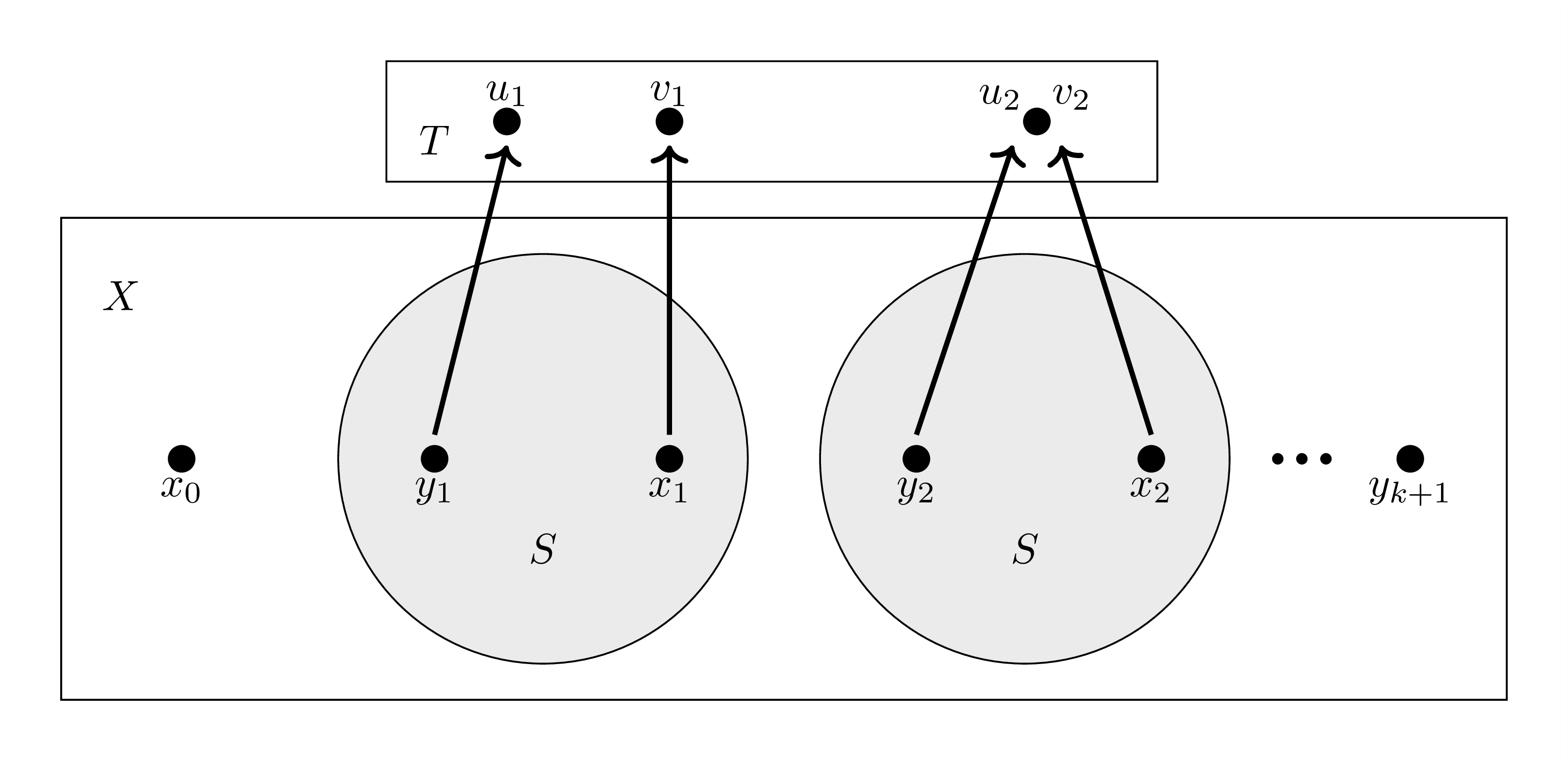 |
Abstract. We introduce a type of surgery on metric spaces. This surgery, in some sense, seeks to replace a subspace S of a metric space X with another metric space T via a function f : S → T. When T is a discrete space, this amounts to collapsing the subspace according to the function. This surgery results in a new metric space we denote X̂f and there is a natural function F : X → X̂f induced from f. Our primary interest is investigating if properties of the original function f are inherited by the induced function F. We show that if f is a pseudo-isometry then so is F. However, for a quasi-isometry, a very natural generalization of a pseudo-isometry that is prevalent in geometric group theory, such a result does not hold. |
 |
Abstract. Suppose G is a free product G = A1 * A2 * ... * FN, where each of the groups Ai is torsion-free and FN is a free group of rank N. Let O be the deformation space associated to this free product decomposition. We show that the diameter of the projection of the subset of O where a given element has bounded length to the Z−factor graph is bounded, where the diameter bound depends only on the length bound. This relies on an analysis of the boundary of G as a hyperbolic group relative to the collection of subgroups Ai together with a given non-peripheral cyclic subgroup. The main theorem is new even in the case that G = FN, in which case O is the Culler−Vogtmann outer space. In a future paper, we will apply this theorem to study the geometry of free group extensions. |
 |
Abstract. An expository article on geometric group theory, focusing on negative curvature in groups. |
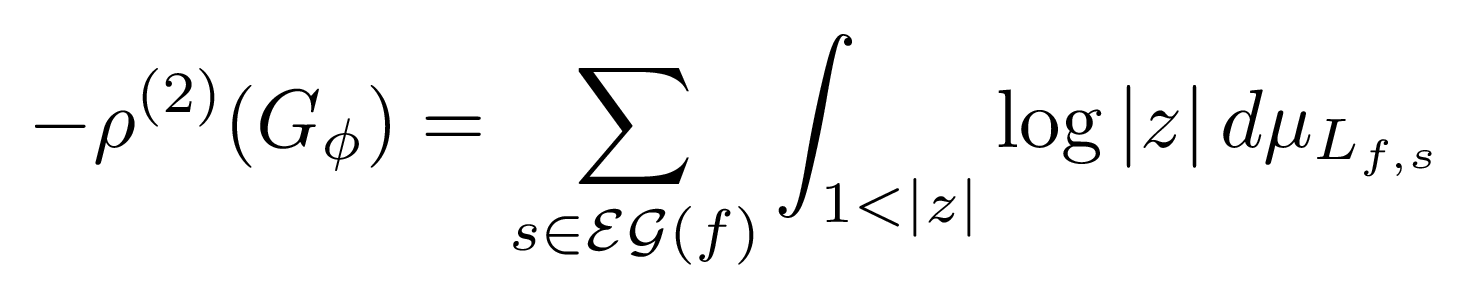 |
Abstract. We introduce a condition on the monodromy of a free-by-cyclic group, Gφ, called the chain flare condition, that implies that the L2–torsion, ρ(2)(Gφ), is non-zero. We conjecture that this condition holds whenever the monodromy is exponentially growing. |
 |
Abstract. In this paper we consider two piecewise Riemannian metrics defined on the Culler–Vogtmann outer space which we call the entropy metric and the pressure metric. As a result of work of McMullen, these metrics can be seen as analogs of the Weil–Petersson metric on the Teichmüller space of a closed surface. We show that while the geometric analysis of these metrics is similar to that of the Weil–Petersson metric, from the point of view of geometric group theory, these metrics behave very differently to the Weil–Petersson metric. Specifically, we show that when the rank r is at least 4, the action of Out(𝔽r) on the completion of the Culler–Vogtmann outer space using the entropy metric has a fixed point. A similar statement also holds for the pressure metric. |
| Abstract. Let G be a free-by-cyclic group or a 2–dimensional right-angled Artin group. We provide an algebraic and a geometric characterization for when each aspherical simplicial complex with fundamental group isomorphic to G has minimal volume entropy equal to 0. In the nonvanishing case, we provide a positive lower bound to the minimal volume entropy of an aspherical simplicial complex of minimal dimension for these two classes of groups. Our results rely upon a criterion for the vanishing of the minimal volume entropy for 2–dimensional groups with uniform uniform exponential growth. This criterion is shown by analyzing the fiber π1–growth collapse and non-collapsing assumptions of Babenko–Sabourau. |
 |
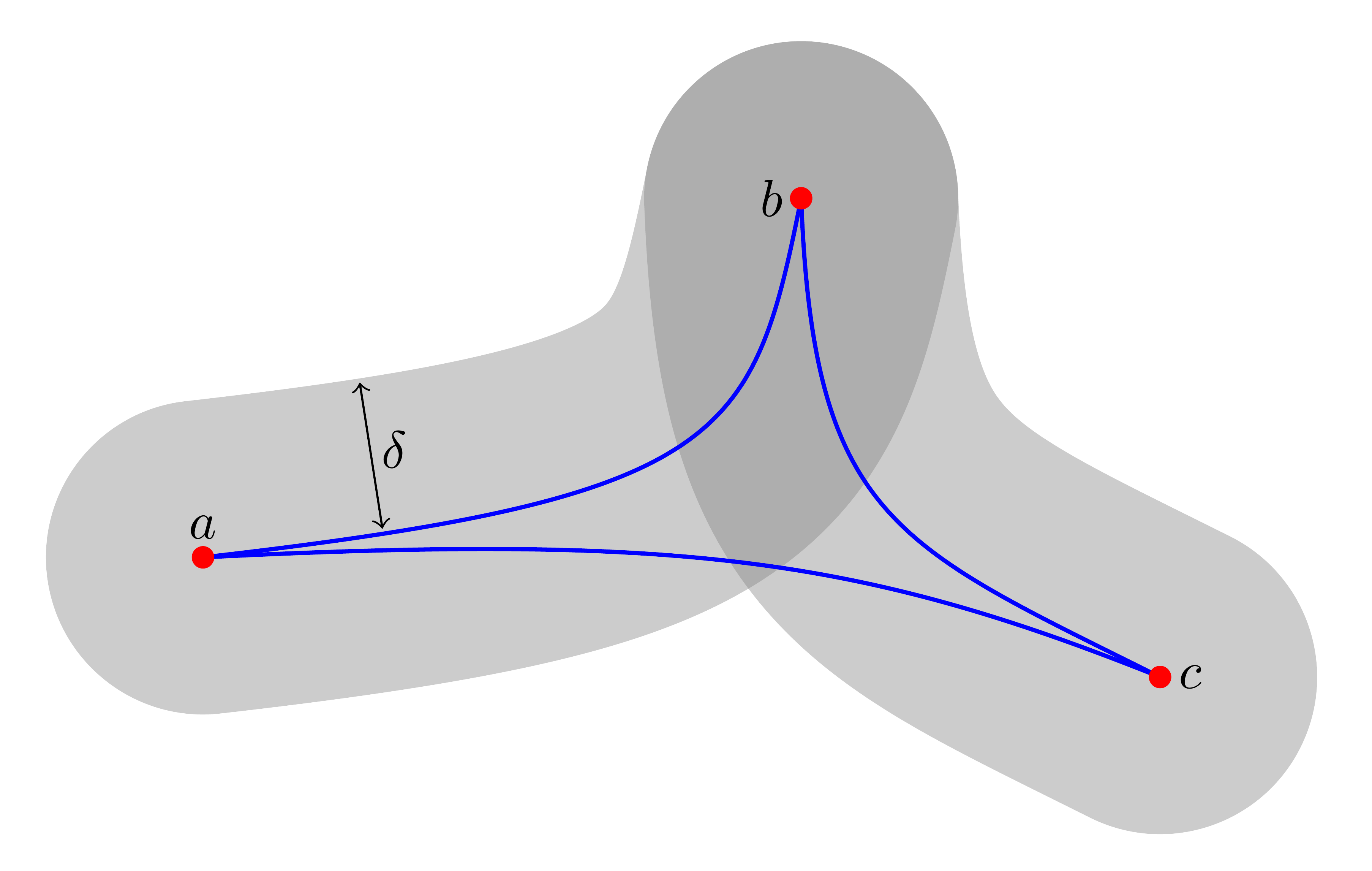
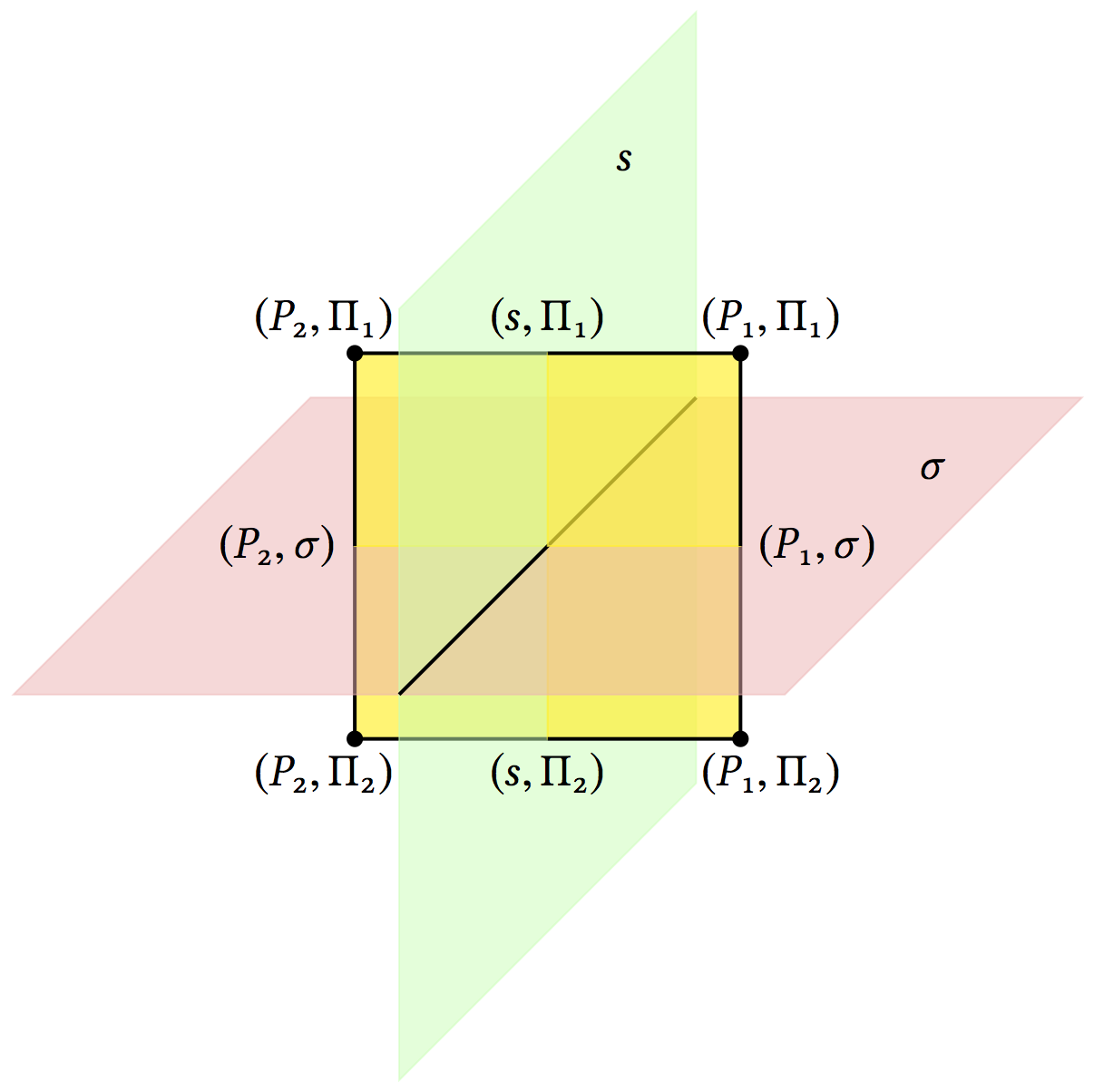
Abstract. This paper is a continuation of our previous work with Margalit where we studied group actions on projection complexes. In that paper, we demonstrated sufficient conditions so that the normal closure of a family of subgroups of vertex stabilizers is a free product of certain conjugates of these subgroups. In this paper, we study both the quotient of the projection complex by this normal subgroup and the action of the quotient group on the quotient of the projection complex. We show that under certain conditions that the quotient complex is 𝛿–hyperbolic. Additionally, under certain circumstances, we show that if the original action on the projection complex was a non-elementary WPD action, then so is the action of the quotient group on the quotient of the projection complex. This implies that the quotient group is acylindrically hyperbolic. |
 |
Abstract. We construct the first examples of normal subgroups of mapping class groups that are isomorphic to non-free right-angled Artin groups. Our construction also gives normal, non-free right-angled Artin subgroups of other groups, such as braid groups and pure braid groups, as well as most subgroups of the mapping class group, such as the Torelli subgroup. Our work recovers and generalizes the seminal result of Dahmani–Guirardel–Osin, which gives free, purely pseudo-Anosov normal subgroups of mapping class groups. We give two applications of our methods: (1) we produce an explicit proper normal subgroup of Mod(S) that is not contained in any level m congruence subgroup, and (2) we produce an explicit an example of a pseudo-Anosov mapping class with the property that all of its even powers have free normal closure and its odd powers normally generate the entire mapping class group. The technical theorem at the heart of our results is a new version of the windmill apparatus of Dahmani–Guirardel–Osin, which is tailored to the setting of group actions on the projection complexes of Bestvina–Bromberg–Fujiwara. |
 |
Abstract. We show that for any subgroup ℋ of Out(FN), either ℋ contains an atoroidal element or a finite index subgroup ℋ' of ℋ fixes a nontrivial conjugacy class in FN. This result is an analog of Ivanov's subgroup theorem for mapping class groups and Handel–Mosher's subgroup theorem for Out(FN) in the setting of irreducible elements. |
 |
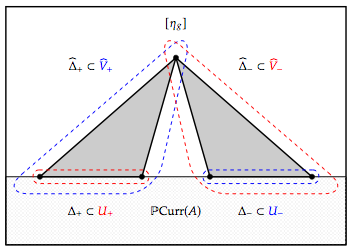
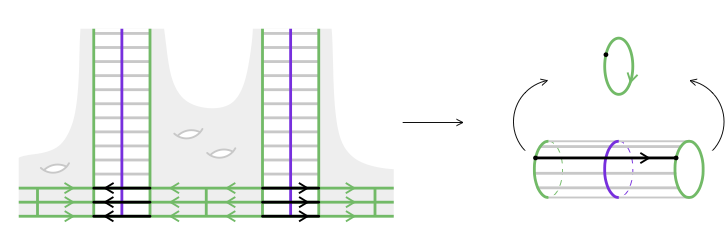
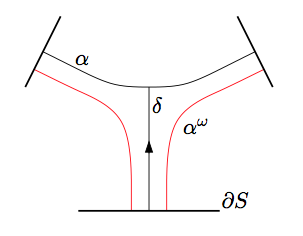
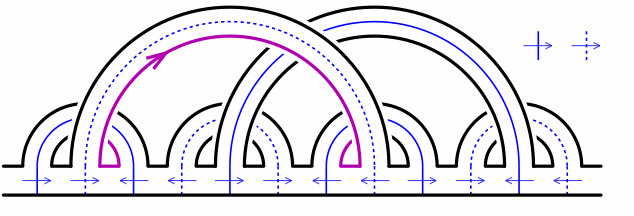
Abstract. We show that the Hausdorff distance between any forward and any backward surgery paths in the sphere graph is at most 2. From this it follows that the Hausdorff distance between any two surgery paths with the same initial sphere system and same target sphere system is at most 4. Our proof relies on understanding how surgeries affect the Guirardel core associated to sphere systems. We show that applying a surgery is equivalent to performing a Rips move on the Guirardel core. |
| Abstract. Given isometric actions by a group G on finitely many δ−hyperbolic metric spaces, we provide a sufficient condition that guarantees the existence of a single element in G that is hyperbolic for each action. As an application we prove a conjecture of Handel and Mosher regarding relatively fully irreducible subgroups and elements in the outer automorphism group of a free group. |
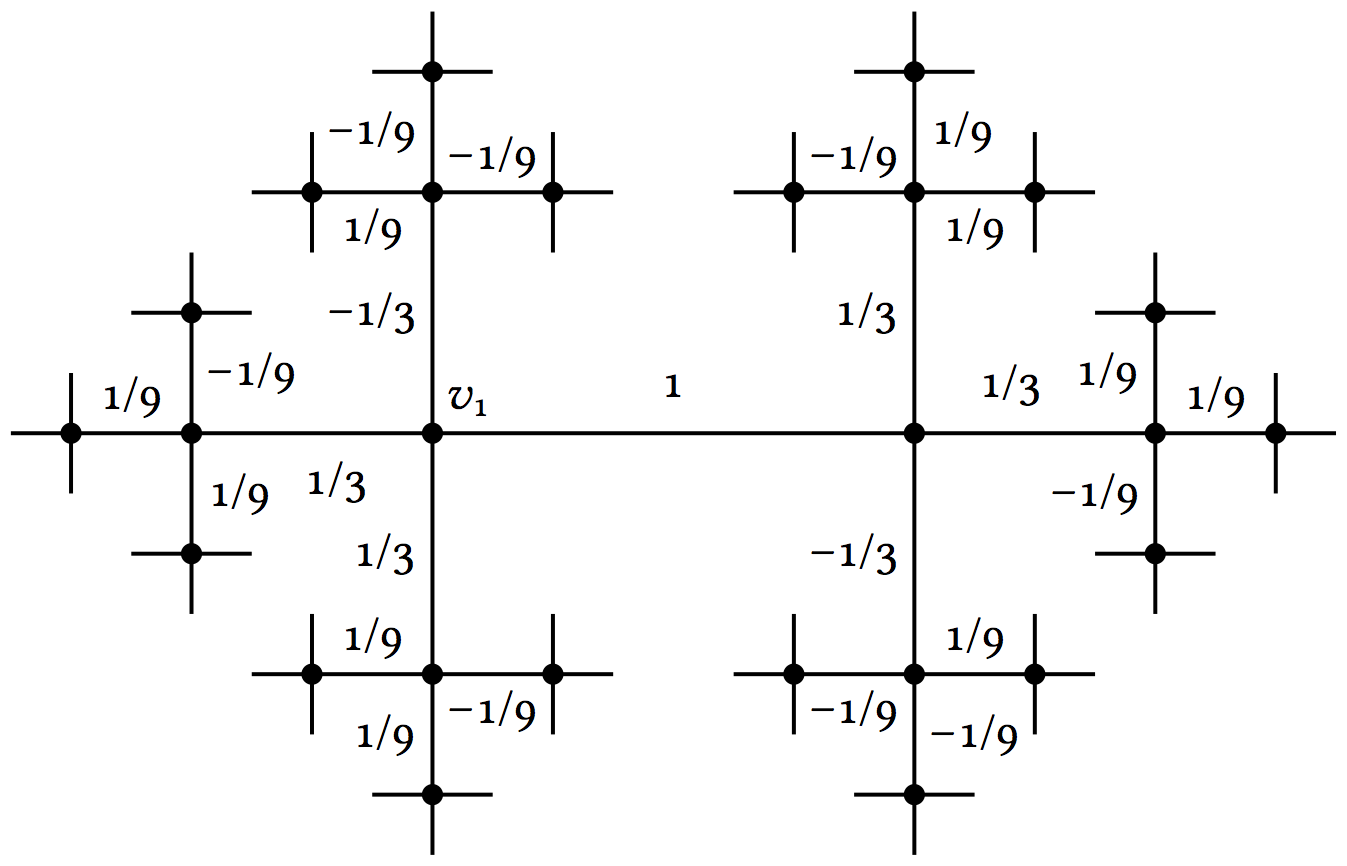 |
Abstract. We analyze the reduced ℓ²−homology of a finitely generated nonabelian free group, 𝔽. Specifically, the projection map onto the space of harmonic ℓ²−1−chains is explicitly described and a weak isomorphism from (ℓ²(𝔽))rk(𝔽)−1 to the space of harmonic ℓ²−1−chains is given. |
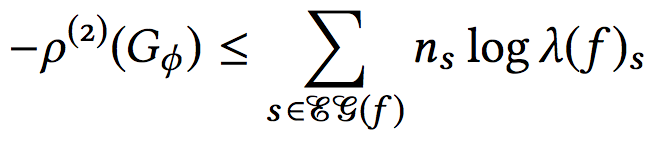 |
Abstract. We provide an upper bound on the ℓ²−torsion of a free-by-cyclic group, −ρ(2)(𝔽 ⋊Φ ℤ), in terms of a relative train-track representative for Φ ∈ Aut(𝔽). Our result shares features with a theorem of Lück−Schick computing the ℓ²−torsion of the fundamental group of a 3−manifold that fibers over the circle in that it shows that the ℓ²−torsion is determined by the exponential dynamics of the monodromy. In light of the result of Lück−Schick, a special case of our bound is analogous to the bound on the volume of a 3−manifold that fibers over the circle with pseudo-Anosov monodromy by the normalized entropy recently demonstrated by Kojima−McShane. |
 |
Abstract. We show that a right-angled Artin group, defined by a graph Γ that has at least three vertices, does not split over an infinite cyclic subgroup if and only if Γ is biconnected. Further, we compute JSJ−decompositions of 1−ended right-angled Artin groups over infinite cyclic subgroups. |
| Abstract. We provide an effective algorithm for determining whether an element φ of the outer automorphism group of a free group is fully irreducible. Our method produces a finite list which can be checked for periodic proper free factors. |
 |
Abstract. This paper has two
parts, on Baumslag−Solitar groups and on general
G−trees. In the first part we establish bounds for stable commutator length (scl) in Baumslag−Solitar groups. For a certain class of elements, we further show that scl is computable and takes rational values. We also determine exactly which of these elements admit extremal surfaces. In the second part we establish a universal lower bound of 1/12 for scl of suitable elements of any group acting on a tree. This is achieved by contructing efficient quasimorphisms. Calculations in the group BS(2, 3) show that this is the best possible universal bound, thus answering a question of Calegari and Fujiwara. We also establish scl bounds for acylindrical tree actions. Returning to Baumslag−Solitar groups, we show that their scl spectra have a uniform gap: no element has scl in the interval (0, 1/12). |
| Abstract. We prove that, aside from the obvious exceptions, the mapping class group of a compact orientable surface is not abstractly commensurable with any right-angled Artin group. Our argument applies to various subgroups of the mapping class group−the subgroups generated by powers of Dehn twists and the terms of the Johnson filtration−and additionally to the outer automorphism group of a free group and to certain linear groups. |
 |
Abstract. We prove that the curve graph C(1)(S) is Gromov-hyperbolic with a constant of hyperbolicity independent of the surface S. The proof is based on the proof of hyperbolicity of the free splitting complex by Handel and Mosher, as interpreted by Hilion and Horbez. |
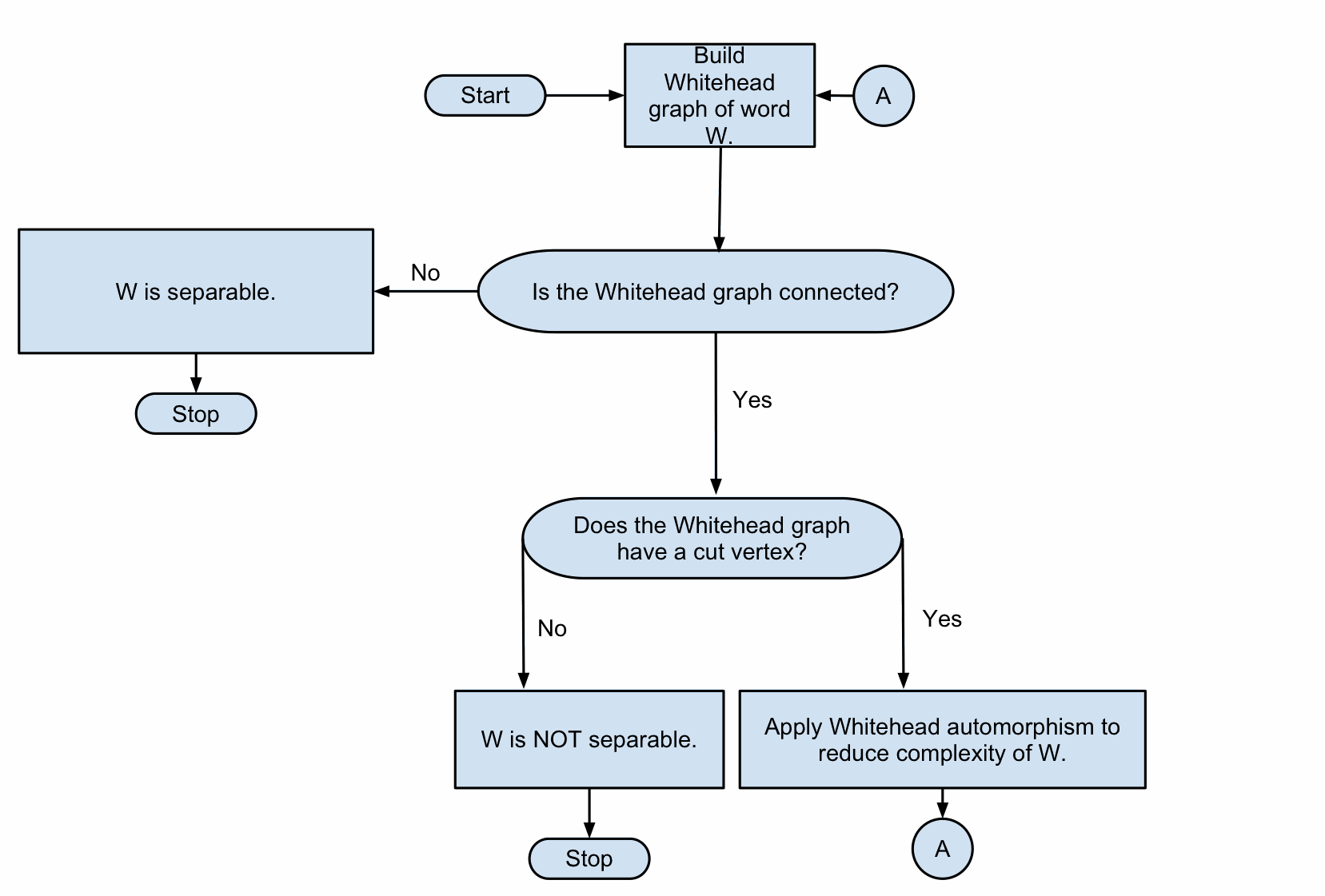 |
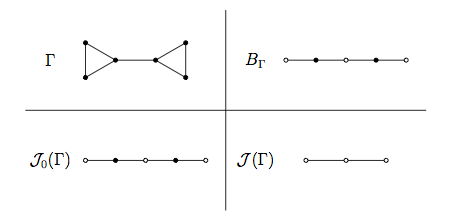
Abstract. By applying an algorithm of Stallings regarding separability of elements in a free group, we give an alternative approach to that of Osborne and Zieschang in describing all primitive elements in the free group of rank 2. As a result, we give a proof of a classical result of Nielsen, used by Osborne and Zieschang in their work, that the only automorphisms of F2 that act trivially on the abelianization are those defined by conjugation. Finally, we compute the probability that a Whitehead graph in rank 2 contains a cut vertex. We show that this probability is approximately 1/ℓ2 where ℓ is the number of edges in the graph. |
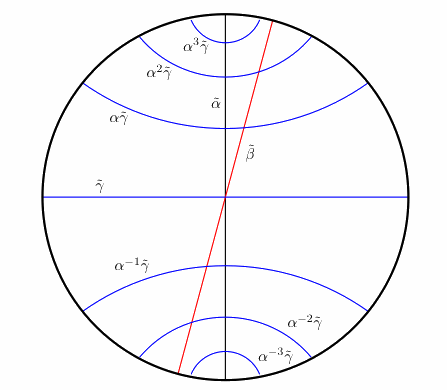 |
Abstract. Subsurface projection has become indispensable in studying the geometry of the mapping class group and the curve complex of a surface. When the subsurface is an annulus, this projection is sometimes called relative twisting. We give two alternate versions of relative twisting for the outer automorphism group of a free group. We use this to describe sufficient conditions for when a folding path enters the thin part of Culler−Vogtmann's Outer space. As an application of our condition, we produce a sequence of fully irreducible outer automorphisms whose axes in Outer space travel through graphs with arbitrarily short cycles; we also describe the asymptotic behavior of their translation lengths. |
 |
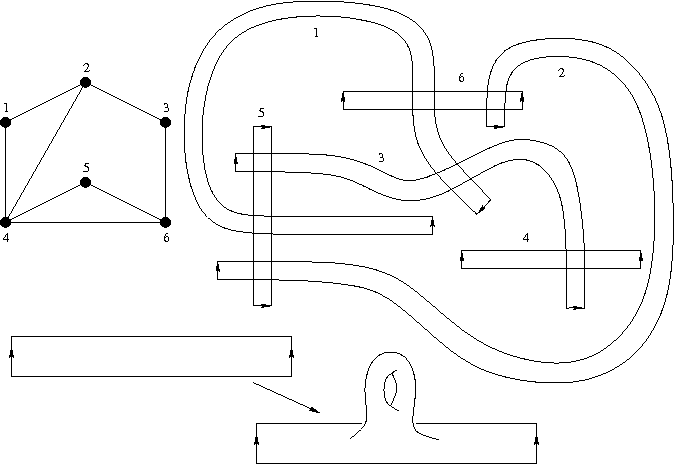
Abstract. This notes provides an alternative account of Calegari's rationality theorem for stable commutator length in free groups. |
 |
Abstract. We describe sufficient conditions which guarantee that a finite set of mapping classes generate a right-angled Artin group quasi-isometrically embedded in the mapping class group. Moreover, under these conditions, the orbit map to Teichmüller space is a quasi-isometric embedding for both of the standard metrics. As a consequence, we produce infinitely many genus h surfaces (for any h at least 2) in the moduli space of genus g surfaces (for any g at least 3) for which the universal covers are quasi-isometrically embedded in the Teichmüller space. |
| Abstract. We show for k ≥ 3, given any matrix in GL(k, ℤ) there is a hyperbolic fully irreducible automorphism of the free group of rank k whose induced action on ℤk is the given matrix. |
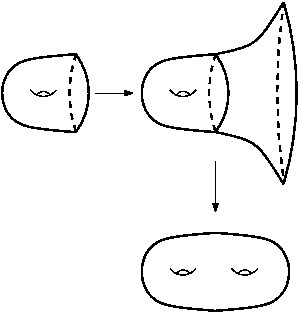 |
Abstract. By a theorem of Thurston, in the subgroup of the mapping class group generated by Dehn twists around two curves which fill, every element not conjugate to a power of one of the twists is pseudo-Anosov. We prove an analogue of this theorem for the outer automorphism group of a free group. |
 |
Abstract. We construct a
hyperbolic group containing a finitely presented subgroup, which has
infinitely many conjugacy classes of finite-orider elements.
We also use a version of Morse theory with high dimensional horizontal cells and use handle cancellation arguments to produce other examples of subgroups of CAT(0) groups with infinitely many conjugacy classes of finite-order elements. |
 |
Abstract. For a fully irreducible automorphism φ of the free group Fk we compute the asymptotics of the intersection number n → i(T,T'φn) for trees T, T' in Outer space. We also obtain qualitative information about the geometry of the Guirardel core for the trees T and T'φn for n large. |
 |
Abstract. We construct a
CAT(0) group containing a finitely presented subgroup with
infinitely many conjugacy classes of finite-order elements. Unlike
previous examples (which were based on right-angled Artin groups)
our ambient CAT(0) group does not contain any rank 3 free abelian
subgroups. We also construct examples of type Fn inside mapping class groups, Aut(Fk), and Out(Fk) which have infinitely many conjugacy classes of finite-order elements. |
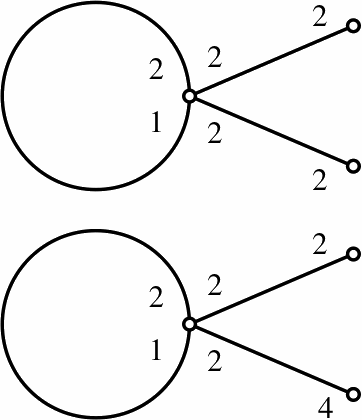 |
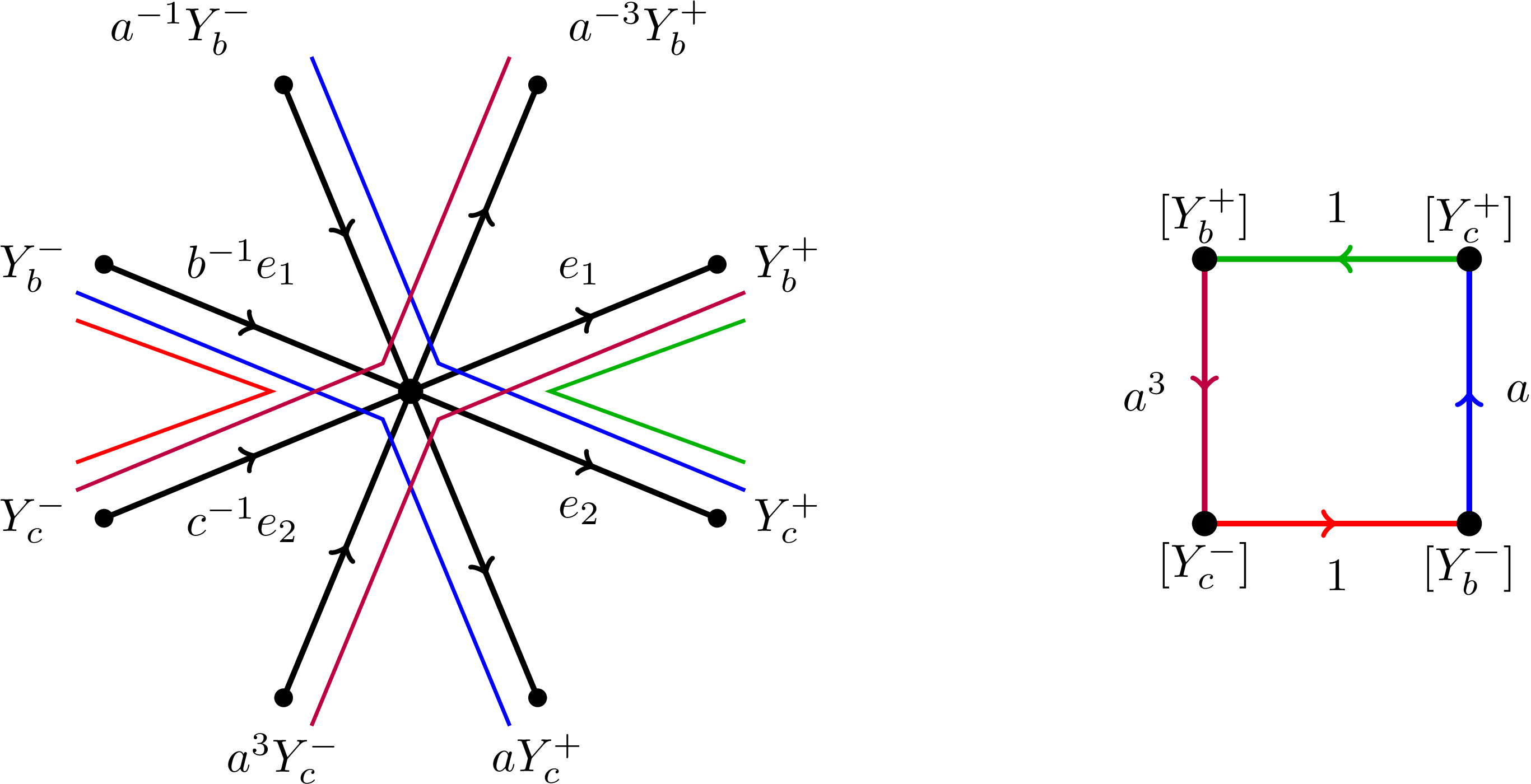
Abstract. Generalized Baumslag-Solitar groups (GBS groups) are groups that act on trees with infinite cyclic edge and vertex stabilizers. Such an action is described by a labeled graph (essentially, the quotient graph of groups). This paper addresses the problem of determining whether two given labeled graphs define isomorphic groups; this is the isomorphism problem for GBS groups. There are two main results and some applications. First, we find necessary and sufficient conditions for a GBS group to be represented by only finitely many labeled graphs. These conditions can be checked effectively from any labeled graph. Then we show that the isomorphism problem is solvable for GBS groups whose labeled graphs have Betti number at most one. |
 |
Abstract. We generalize the familiar notion of a Whitehead move from Culler and Vogtmann's Outer space to the setting of deformation spaces of G−trees. Specifically, we show that there are two moves, each of which transforms a reduced G−tree into another reduced G−tree, that suffice to relate any two reduced trees in the same deformation space. There two moves further factor into three moves between reduced trees that have simples descriptions in terms of graphs of groups. This result has several applications. |
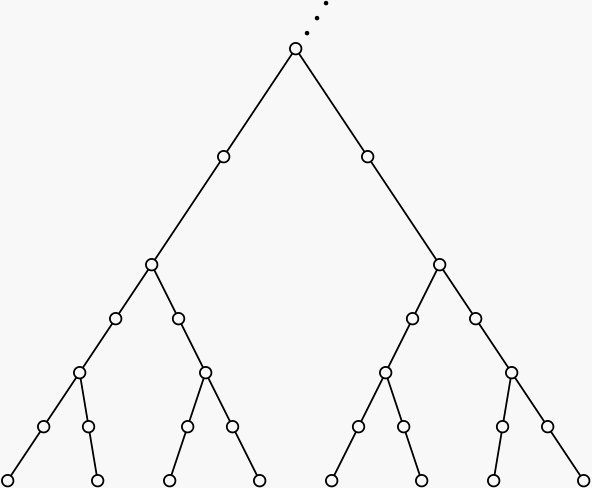 |
Abstract. We construct an invariant deformation retract of a deformation space of G-trees. We show that this complex is finite dimensional in certain cases and provide an example that is not finite dimensional. Using this complex we compute the automorphism group of the classical non-solvable Baumslag-Solitar groups BS(p,q). The most interesting case is when p properly divides q. Collins and Levin computed a presentation for Aut(BS(p,q)) in this case using algebraic methods. Our computation uses Bass-Serre theory to derive these presentations. Additionally, we provide a geometric argument showing Out(BS(p,q)) is not finitely-generated when p properly divides q. |
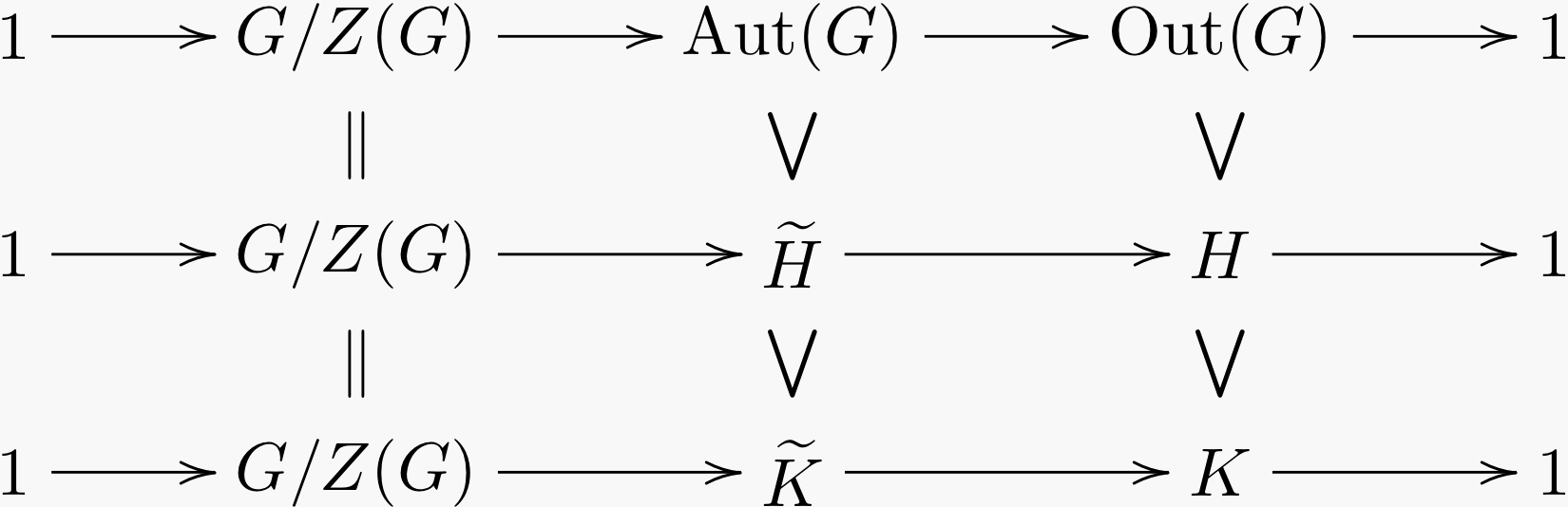 |
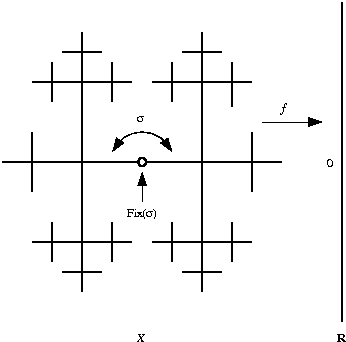
Abstract. For a finitely generated free group Fn, of rank at least 2, any finite subgroup of Out(Fn) can be realized as a group of automorphisms of a graph with fundamental group Fn. This result is known as Out(Fn) Realization. This theorem is comparable to Nielsen Realization as proved by Kerchoff: for a closed surface with negative Euler characteristic, any finite subgroup of the mapping class group of the surface can be realized as a group of isometries of a hyperbolic surface. Both of these theorems have restatements in terms of fixed points. For nonnegative integers n we define a class of groups and prove a similar statement for their outer automorphism groups. |
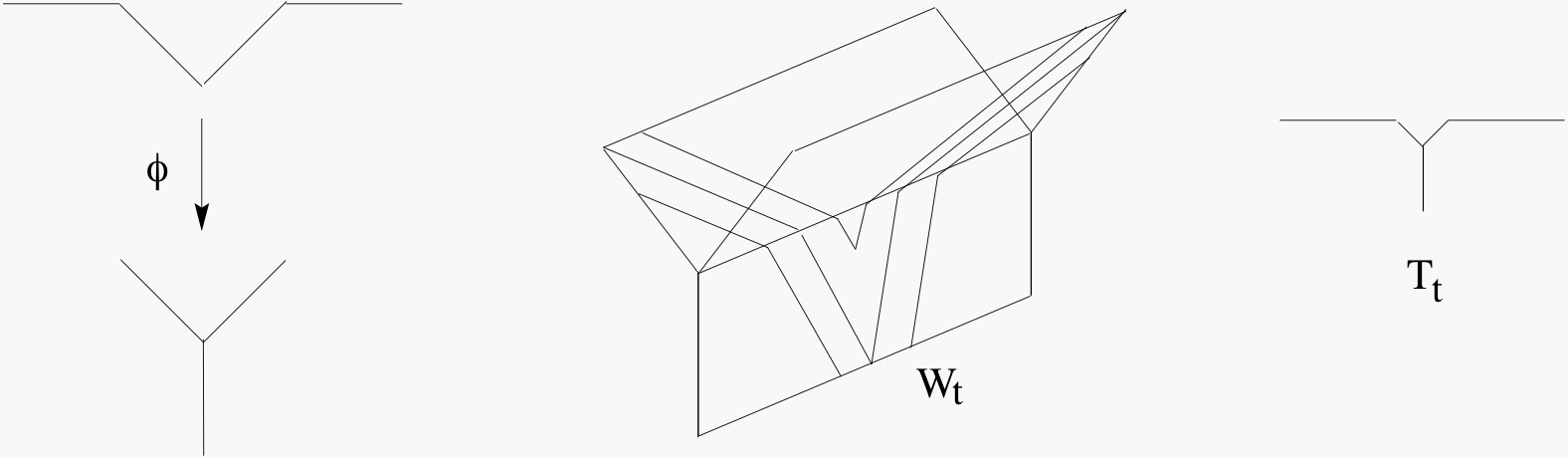 |
Abstract. Forester has defined spaces of simplicial tree actions for a finitely generated group, called deformation spaces. Culler and Vogtmann's Outer space is an example of a deformation space. Using ideas from Skora's proof of the contractibility of Outer space, we show that under some mild hypotheses deformation spaces are contractible. |
