The Laplace transform allows us to solve initial value problems arising from mass/spring/dashpot systems with a piecewise driving force. For example, consider the following IVP that models a mass/spring system (no resistance):
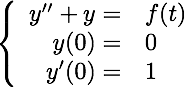
where:
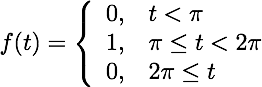
Applying the Laplace transform to the IVP and solving for Y(s), the Laplace transform of y, we obtain:
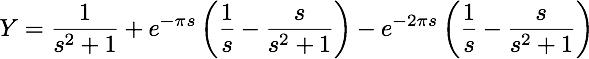
Hence, applying the inverse Laplace transform to Y, we find the solution to the IVP is:
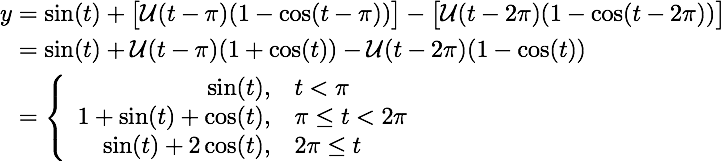
The pulse driving force f (t) and solution y (t) are shown below.
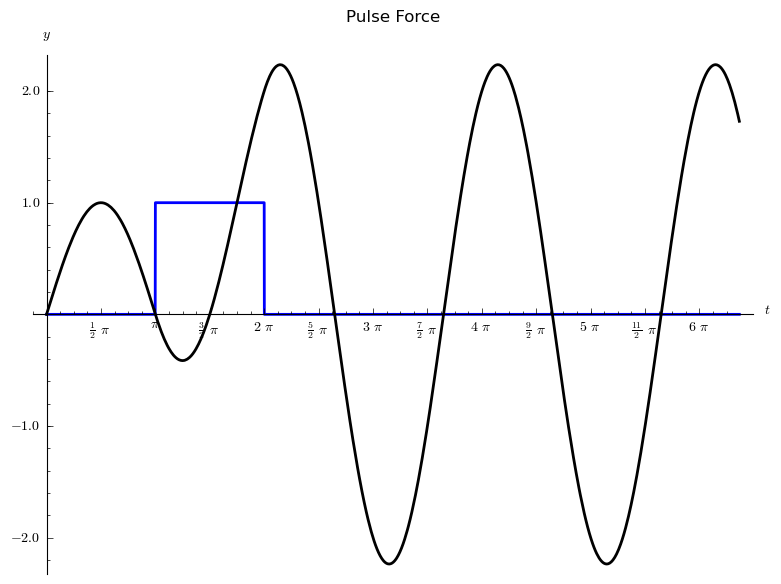
We also present another example. This one includes resonance. Consider the following IVP that also models a mass/spring system (no resistance):
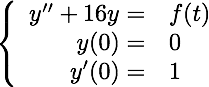
where:
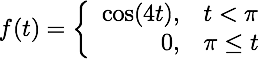
As before, we apply the Laplace transform to the IVP and solve for Y(s), the Laplace transform of y. We obtain:
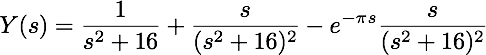
Hence, applying the inverse Laplace transform to Y, we find the solution to the IVP is:
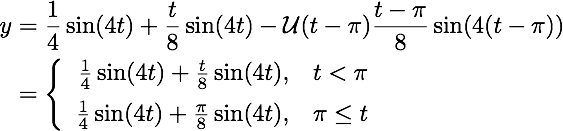
The pulse driving force f (t) and solution y (t) are shown below.
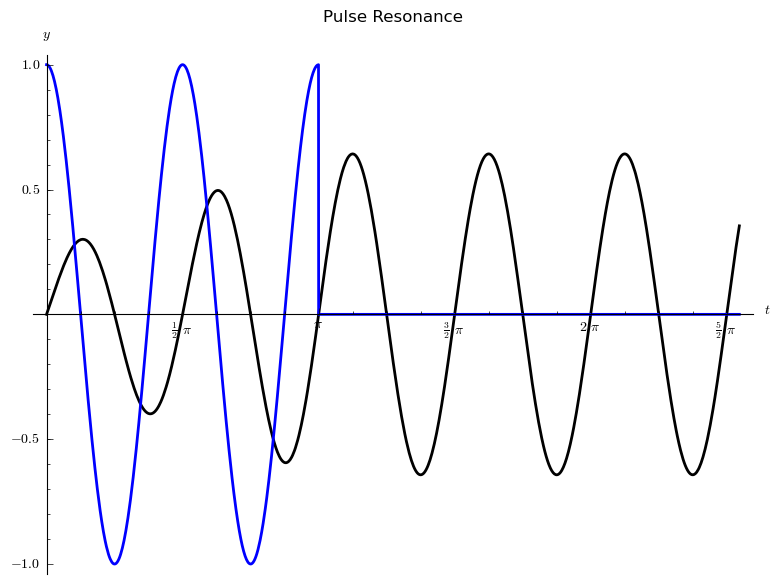
Images generated by sage.