The Gamma function, denoted Γ(α), is defined for positive real numbers by an integral formula:
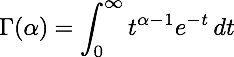
Two computations help to illustrate the usefulness of this function.
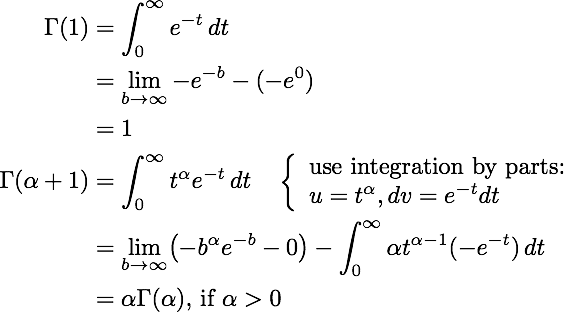
Thus we see that Γ(2) = 1⋅Γ(1) = 1, Γ(3) = 2⋅Γ(2) = 2, Γ(4) = 3⋅Γ(3) = 3 ⋅ 2 = 6, Γ(5) = 4⋅Γ(4) = 4 ⋅ 3 ⋅ 2 = 24, ... and so on. Hence we get the formula: Γ(n+1) = n!.
It is not obvious, but Γ(α) extends to a "nice" function for all values of α except 0, −1, −2, −3, ... and the above formula (Γ(α + 1) = αΓ(α)) holds for all of these values of α too. Below is shown a plot of the Gamma function along with the factorial function.
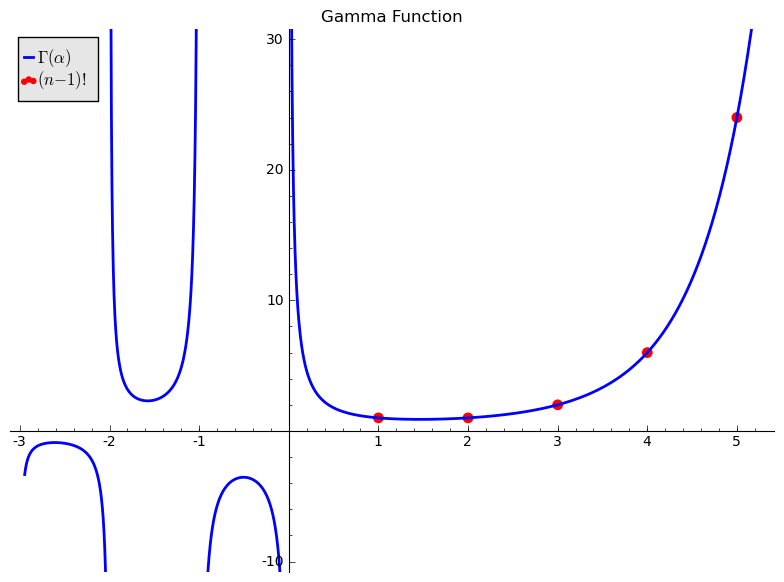
Images generated by sage.