Free Damped Motion

Free damped motion of a mass m is modeled by the 2nd order ODE:

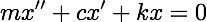
where x(t) is the distance from equilibrium, c is the damping constant and k is the spring constant. We divide by m and write:

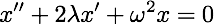
where 2λ = c/m and ω² = k/m. The qualitative nature of the solution depends on whether λ is greater than, equal to or less than ω.

Overdamped (λ > ω): The roots of the auxiliary equation are −λ ± (λ² − ω²)^½ and so the general solution is:

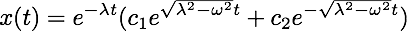
Critically Damped (λ = ω): The auxiliary equation has −λ as a repeated root and so the general solution is:

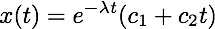
Underdamped (λ < ω): The roots of the auxiliary equation are the complex numbers −λ ± iω₀ where ω₀ = (ω² − λ²)^½ and so the general solution is:

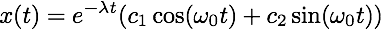
Solution curves in the three cases and also the undamped case (c = 0) are shown below. These functions all satisfy the initial conditions x(0) = 6 and x'(0) = 0

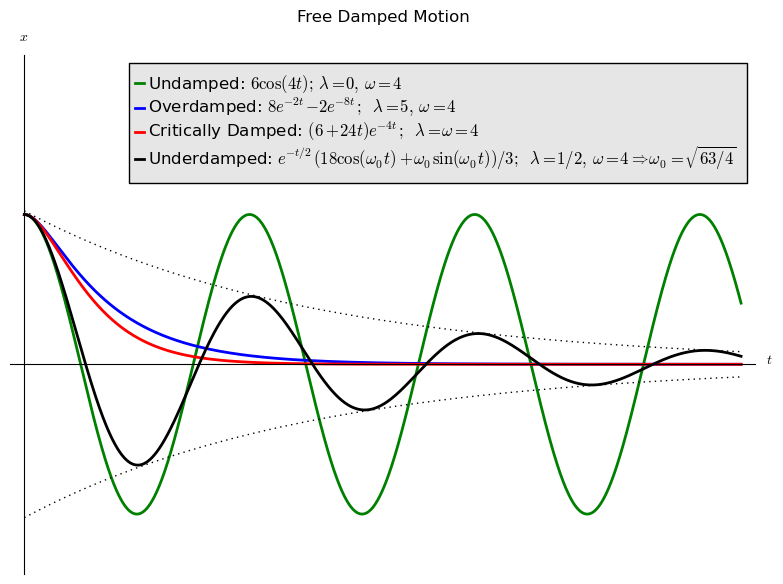
Notice that the frequency in the underdamped case (ω₀) is slightly less than in the undamped case (ω); we see this in the slightly longer wavelength in the underdamped case. The dotted black line is the "exponential envelop" ±(6² + (ω₀/3)²)^½e^−t/2.

Images generated by sage.