Coupled Mass/Spring System

Consider the coupled mass/spring system:

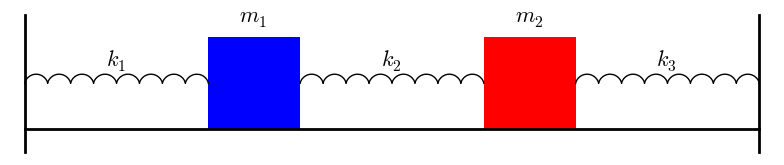
where m₁ = 1, m₂ = 2 and k₁ = 1, k₂ = k₃ = 2. This is modeled by the system of differential equations:

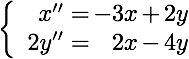
Written in operator form we have:

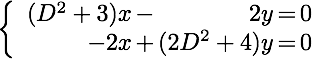
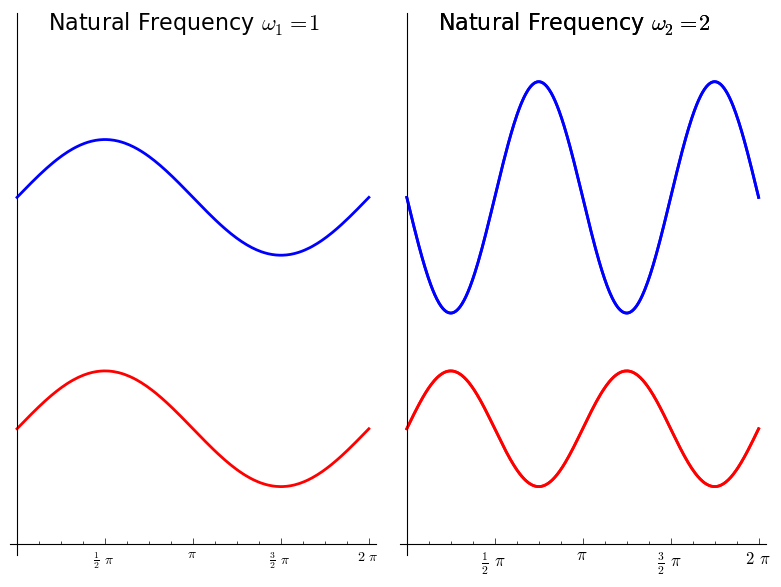
The general solution has two natural frequencies ω₁ = 1, ω₂ = 2 and can be expressed as:

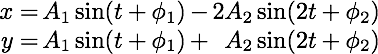
In the first natural mode, the masses oscillate in the same direction with the same amplitude; in the second natural mode the masses oscillate in the opposite direction and the amplitude of the first mass is twice the amplitude of the second.

Fixing some initial conditions for the masses: x(0) = −1, x'(0) = −3, and y(0) = 2, y'(0) = 3, we have the solution:

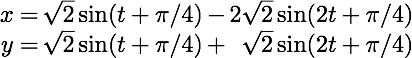
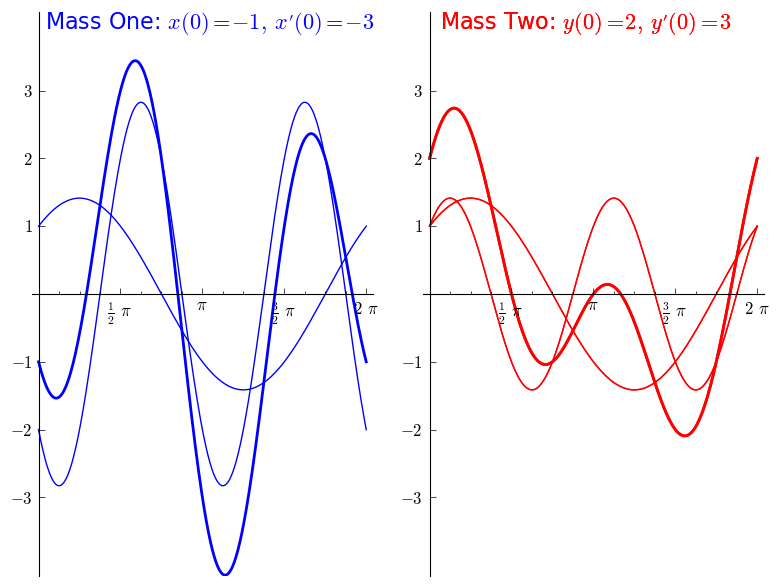
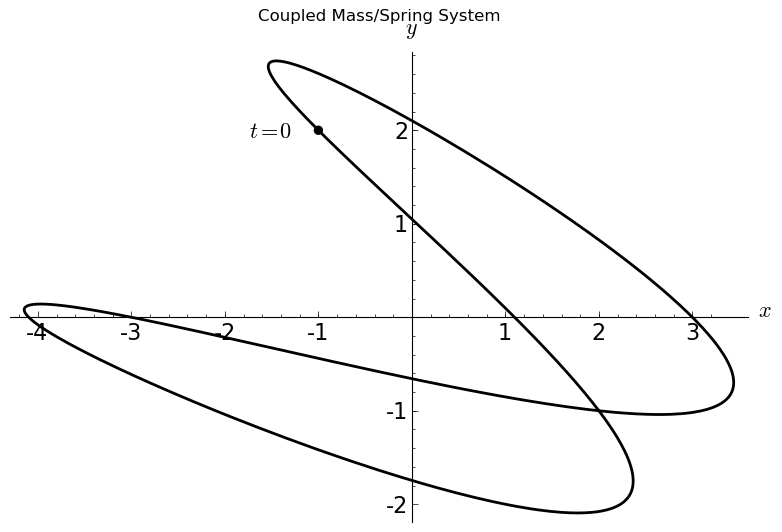
The phase diagram for the system is shown below:

Images generated by sage.