Boundary Value Problems

The 2nd order ODE:

y'' + y = 0

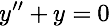
has a two-parameter family of solutions:

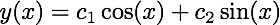
y(x) = c_1cos(x) + c_2sin(x)

Solutions such that y(0) = 0 necessarily are of the form: y(x) = c2 sin(x). Examples of these curves are shown below:

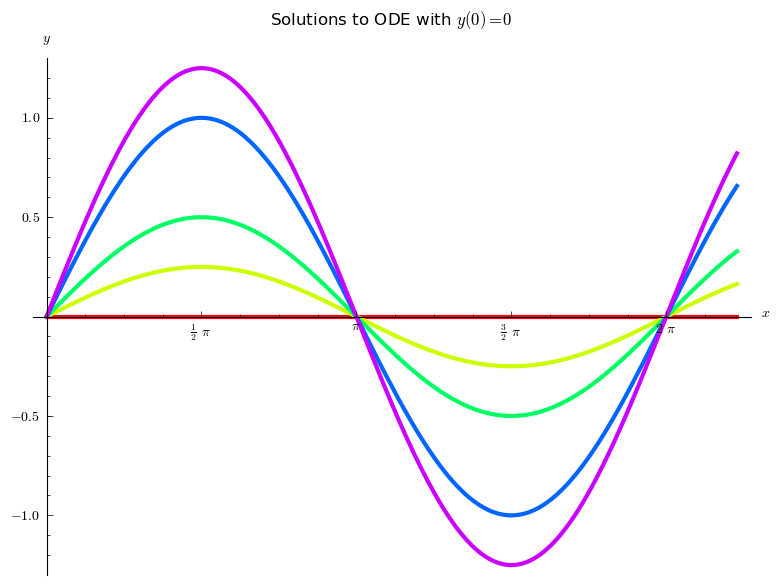
Solution curves to BVP with y(0) = 0

c2 = 0, ¼, ½, 1, 1.25

We can define an IVP by imposing y'(0) = y1. The unique solution to the IVP is y(x) = y1 sin(x).

We can define a BVP by imposing y(x1) = y1. If x1 is not a multiple of π, there is a unique solution. If x1 is a multiple of π, there is no solution unless y1 = 0, in which case every curve y(x) = c2 sin(x) is a solution.


Images generated by sage.